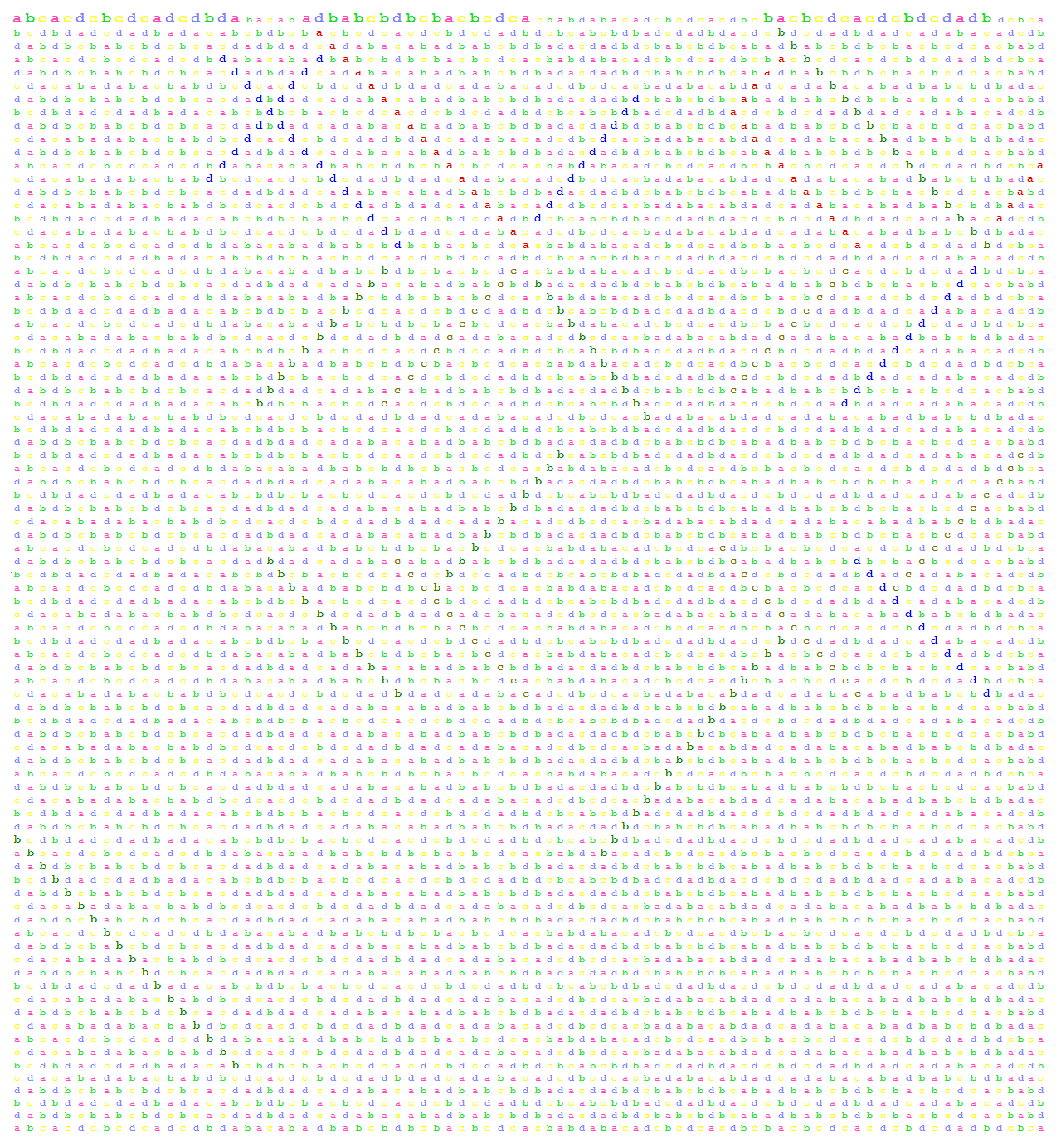
We apply the endomorphism  g  over four letters  { a,b,c,d }  to  g85(a),  where  g  
is defined by the productions  g:  a → g85a,  b → g85b,  c → g85d,  d → g85c.
The word obtained, i.e.,  g(g85(a)),  is represented by a  85 x 85  matrix.
    
Below we put colour on letters and highlight some diagonals that indicate
permutative reappearance of quite long factors of  g85(a).  The factors
do not reappear as such but in the structural sense, i.e., with letters renamed.

Backwords leaning diagonals represent reappearances of previous factors in the form of semi-mirror images.  

Those backwords leaning diagonals that cross the main diagonal represent semi-palindrome factors of  g85(a).
    
© 2004 V. Keränen  
Permission to use, copy, and distribute this material for any non-commercial purpose is
hereby granted without a separate permission, provided that the source is mentioned.

Created by Mathematica  (October 6, 2004)